Для численного решения уравнения (16.99), как и для решения уравнения (16.96), можно использовать прямые и итерационные методы.

Весь алгоритм расчета можно представить следующим образом. Решение уравнений (16.80) -(16.83) получается за один

экспериментальные данные Спэрроу -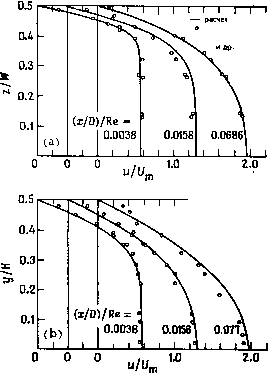

I I I [ I [ - расчет о экспериментальные

данные Спэрроу ~ и др.

Рис. 16.13. Распределение осевой скорости в канале с удлинением W/H==2.0 ([Briley, 1974]; печатается с разрешения Academic Press).

проход вниз ПО потоку, в каждой плоскости а: + значения ft+i yft+i p/l и р + определяются следующим об-

разом:

1) решение уравнений (16.88), (16.89) и (16.92) позволяет определить и- pyj и w;

2) решение уравнений (16.96), (16.94) и (16.93) позволяет определить v+ и w -;

3) решение уравнения (16.99) позволяет определить

Общая погрешность всего алгоритма 0(Ал:, Ау, Аг). Несмотря на то что некоторые шаги алгоритма требуют проведения итераций, он в целом является весьма эффективным. По сравнению с задачей о закрученном течении (п. 16.2.1) наличие

масштаб скоростей ДуХ ПОПСреЧНЫХ КООрДИНаТ

Q 2.0 приводит к более сложному

I I I I I Mnii или (a;/(/JRe способу определения v, w и по-

а:

-0.5

-0.5

правки давления при помощи уравнения Пуассона. В задаче о закрученном потоке радиальная скорость и поперечная поправка давления получались за один мар- шевый проход в радиальном направлении.

В работе [Briley, 1974] получено решение для ламинарного течения в канале с отношением сторон 1:1 и 2:1. Типичные результаты для канала с отношением сторон 2: 1 представлены на рис. 16.13 и 16.14. Число Рейнольдса Re, вычисленное по средней скорости на оси Um и гидравлическому диаметру (рис. 16.7), равно 1333. Решения получены на сетке 21X21 в поперечной плоскости. Для прохода вниз по потоку обычно требовалось 75 шагов. Как видно из рис. 16.13, рассчитанные значения осевой со-

Рис. 16.14. Профили вторичных скоростей в канале с удлинением 2 : 1 wvv,ivxx v,v ([Briley, 1974]; печатается с разре- ставляющеи скорости в раз-шения Academic Press). личных поперечных сечениях

хорошо согласуются с экспериментальными данными из работы [Sparrow et. al., 1967]. Можно заметить (рис. 16.14), что вторичные компоненты скорости довольно малы. Большие значения поперечных скоростей получаются при неодинаковом нагреве стенок канала и учете плавучести в уравнении вертикальной поперечной составляющей импульса. Этот случай также рассмотрен в работе [Briley, 1974].

Описанный выше алгоритм в несколько измененном виде использовался для расчета ламинарного течения в прямом по-

лярном канале [Ghia et al., 1977 ном канале [Ghia, Sokhey, 1977

и в искривленном прямоуголь-Обобщение на искривленный

полярный канал описано в работе [Ghia et al., 1979].

Задача о расчете течения в канале за один маршевый проход рассматривалась в работах [Patankar, Spalding, 1972; Rubin et al., 1977; Kreskovsky, Shamroth, 1978; Anderson, 1980; Cooke, Dwoyer, 1983] и ряде других. В работе [Ghia et al., 1981] показано, что если внутреннее устройство канала приводит к отрыву потока, то укороченные уравнения Навье -Стокса дают правильное решение. Однако при этом один маршевый проход заменяется повторяющимися маршевыми итерациями, в которых сохраняется и используется на следующей итерации все поле давления. Такой итерационный подход к решению RNS-уравнений весьма близок к методу, описываемому в п. 16.3.3.

16.2.3. Течение в искривленном канале прямоугольного сечения

Для расчета течения в прямоугольном канале со слабо искривленной осью применим метод, описанный в п. 16.2.2. При малой кривизне поперечные составляющие скорости v и w малы по сравнению с продольной составляющей и. Это соответствует малым изменениям поправки давления р> в формуле (16.84), особенно в направлении течения, что позволяет пренебречь членом др/дх в уравнении составляющей импульса, направленной по потоку.

При большой кривизне оси канала поперечные составляющие скорости V и W могут стать одного порядка с компонентой и, направленной по потоку. Вследствие этого возникают существенные поперечные изменения давления. Расщепление давления, введенное в п. 16.2.2, в этом случае не приводит систему уравнений к неэллиптическому типу и не может обеспечить возможность определения решения за один маршевый проход.

Другой способ получения неэллиптических уравнений, пригодный для течений большой кривизны, предложен в работе [Briley, McDonald, 1984]. В этом методе для заданной геометрии канала в качестве первого приближения используется невязкое решение U, V\ и р\ которое далее модифицируется путем решения RNS-уравнений, что позволяет учесть вязкие эффекты.

Поперечные компоненты скорости расщепляются следующим образом:

у = к + Уф -f Уг!), ш = + а; + (16.103)

или в векторной форме

v = V + V0 + v, (16.104)