где каждый член v состоит из двух компонент (и, ку). Потенциальная поправка скорости уф = {Уф, уиф} создается градиентом продольной составляющей скорости ди/дх. Ее введение, как и в (16.95), необходимо для выполнения уравнения неразрывности (16.80). Вихревая поправка = {у, Wy} создается направленной по потоку компонентой завихренности Q x, которая в декартовых координатах равна

дW dw,u дV dv.

Если невязкое решение потенциальное, то dW/dy - dV/dz = О, Неэллиптические уравнения могут быть получены в связи с тем, что потенциальная поправка скорости мала по сравнению с невязкой V и вихревой v. Это, как будет показано ниже, следует из сравнения порядков различных членов в уравнениях.

Ниже описывается подход для расчета несжимаемых вязких течений в ортогональных координатах; обобщение на сжимаемые вязкие течения в ортогональных координатах описано в работе [Briley, McDonald, 1984]. Ортогональные координаты обозначаются через (, л ?); и, у, Г(У- локальные составляющие скорости вдоль этих координат. Метрические параметры Ль Лг, Лз определяются соотношениями (12.20), т.е.

А? = 4 + У + 4 hl = xl + yl + zl, hl = xl + yl + zlMQ.m)

и вычисляются, как описано в § 12.2, один раз после построения сетки. Эквивалентная декартова система координат получается, если положить xi = у = zi = 1, а все остальные параметры приняты равными нулю. При этом h\=h2 = h=\.

Поперечное поле скоростей и связано с потенциалом ф и поперечной функцией тока г) соотношениями

\ дФ I дФ

1 (М)1 L.£iMI

Для сравнения порядков величин различных членов предполагается, что направленная по потоку координата I совпадает с линиями тока невязкого течения, поэтому V = W = 0. Подстановка выражений (16.107) в уравнении (16.103) дает

При сравнении порядков величин, как и в п. 16.1.1, предполагается, что вязкие эффекты ограничены слоем безразмерной толщины б, малой по сравнению с безразмерным продольным

размером порядка 0(1). Для обезразмеривания используется характерная длина L в осевом направлении. На входе в ка- ал (рис. 16.7) б -толщина пограничного слоя; в областях

Г Л ШуШф,Ю Gib)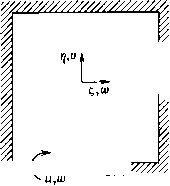

Рис. 16.15. Детали поперечной геометрии.

ВЯЗКОГО и сформировавшегося течений величина б равна половине гидравлического диаметра D.

Метрические параметры Ль Лг, Лз в уравнениях (16.108) порядка 0(1). Вблизи стенки, соответствующей постоянному значению х\ (рис. 16.15),

vO[b\ о (I). (16.109)

Вблизи стенки, соответствующей постоянному значению ,

W ir to(6), о(). (16.110)

Из сопоставления оценок (16.109), (16.110) с выражениями (16.107) следует, что ф имеет порядок 0(6), а г) -порядок О (б). Тогда в соответствии с оценкой (16.109)

Уф, Уф О (б), хЮф-О (62), шф О (1).

В соответствии с (16.110)

тф,тО{Ь), иф0{6)у yO(l).

Поскольку сильные градиенты возникают у стенок, на которых t, или ц постоянны, то

Уф-О(б), и, Уф-0(1). (16.111)

Как и можно было ожидать из (16.107), вихревое поле скорости Уф не появляется в уравнении (16.114). Уравнение (16.114) эквивалентно уравнению (16.95), и для его решения пригоден тот же метод (описан после формулы (16.95)).

Предположение (16.111) о малости скалярного потенциала позволяет упростить уравнение (16.113). Конвективный оператор

Т7 ud.vd.wd i\a\\K\

остается без изменений. Однако вектор и, на который он действует, заменяется на вектор и, определяемый в виде

иЯ КЧф, W + w}, (16.116)

т. е. в соответствии с оценкой (16.111) можно отбросить поперечные потенциальные составляющие скорости.

Выражение для вязкой силы F можно записать в виде

F = v2u = VXS, (16.117)

где завихренность й = VX и. Анализ порядков величин позволяет отбросить ди/дх из F\ и производные по л: в поперечных составляющих вектора УХй. Таким образом, выражения для р2 и Ръ приводятся к виду

П\ПГ2 =---, nih2Fs = --, (16.118)

Следовательно, поперечная потенциальная поправка скорости Уф мала по сравнению с компонентой скорости и, направленной по потоку. В то же время поперечная вихревая скорость того же порядка, что и скорость в направлении потока.

Уравнения, эквивалентные (16.80) - (16.83), могут быть записаны в следующем виде:

V.u = 0, (16.112)

M(u. V)u + Vp-.iF = 0, (16.113)

где u = (и, V, w), М - вектор трех уравнений импульса, F - сила, обусловленная вязкими напряжениями.

После подстановки соотношений (16.104) и (16.107) в (16.112) получается уравнение Пуассона для ф. В декартовых координатах оно имеет вид

дФ , дЧ Г ди . дУ , dW-