

 |
 |
Разделы сайта
Читаемое
Обновления Apr-2024
|
Промышленность Ижоры --> Динамика жидкости: уравнения ди . ди dUe , 1 дх ду дх ду-Чх Re [( + й] - с начальными и граничными условиями (15.3), (15.4). См.: Дородницын А. А. Об одном методе решения уравнений ламинарного пограничного слоя.- Журнал прикл механ. и техн. физ., 1960, № 3, с. 111-118. -Яриж. ред. f-, Fy соответственно. В начале итераций F = Fl и т. д., а после достижения сходимости F- = fи т. д. Основное преимущество схемы DCS состоит в жесткой связи между уравнениями неразрывности и импульса. Благодаря этому сходимость второго порядка по I достигается уже при одной итерации по k. Если аналогичная схема реализуется без связи уравнений неразрывности и импульса (CNS на рис. 15.8), то для сходимости второго порядка требуется 19 итераций. Полученные результаты, представленные на рис. 15.8, соответствуют линейно убывающей скорости Ue/Uoo={l -х/Ь). Член /5t])waii пропорционален коэффициенту поверхностного трения Cf, Блотнер [Blottner, 1975b] указывает, что для рассматриваемых на равномерных сетках типичных задач, связанных с ламинарными течениями, схема DCS более эффективна, чем иные схемы Кранка - Николсона, включая и схему ячеек Келлера. § 15.3. Метод Дородницына описания пограничного слоя Для расчета с необходимой точностью некоторых ламинарных течений и практически всех турбулентных требуется вводить вблизи стенки неоднородную сетку. Однако использования неоднородной сетки можно избежать, если принять и (в двумерном случае) в качестве независимой переменной. В этом состоит основная идея методов Крокко [Blottner, 1975а] и Дородницына В методе Дородницына уравнения сводятся к интегральному виду. Это позволяет использовать методы разностей с весами (гл. 5). В этом параграфе будут рассмотрены два метода. Метод Галёркина с конечными элементами (п. 15.3.1) и спектральный метод Галёркина (п. 15.3.3). Метод Дородницына будет использован здесь для описания турбулентного пограничного слоя, описываемого системой уравнений (11.73) - (11.75). Если для описания сдвиговых напряжений Рейнольдса используется вихревая алгебраическая вязкость Vr, уравнения (в безразмерной форме) могут быть записаны в виде + 4 = 0. (15.51) В методе Дородницына вводятся следующие переменные: Уравнения (15.51), (15.52) могут быть переписаны в виде (15.53) ди . dw ди ди u.t д Г/ v \ (15.54) (15.55) dl dr\ Ue dT] L\ V / (Эт) J где Ue = dujdi. Граничные условия имеют вид ы = а = 0 при 11 = 0 и и - \ при ii = c . Взвешенная сумма (15.51) и (15.52) образуется следующим образом: h ( ) X (15.54) + () X (15.55) = О, где fk{u)-весовая (пробная) функция, которую требуется определить. В результате получается (штрих опущен) Интегрирование проводится от ri = О до т) = оо, а ограничена так, что /ife(oo) = 0. Заменяя переменную интегрирования ц на Uy можно получить следующее уравнение: Г = --- 0 ду\ (15.58) Уравнение (15.57) называется уравнением Дородницына турбулентного пограничного слоя. В этом уравнении Г и в являются зависимыми переменными, ахи и -независимыми. Основное преимущество описания Дородницына заключается в том, что при введении однородной по направлению и сетки большая часть точек автоматически размещается вблизи стенки, где решение изменяется наиболее быстро (рис. 15.9). Это особенно важно при рассмотрении турбулентных пограничных 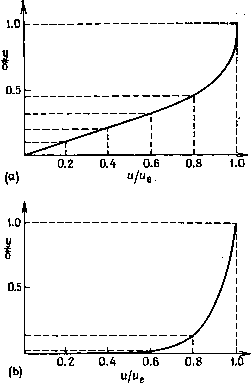 Рис. 15.9. Распределение скорости в ламинарном (а) и турбулентном (Ь) пограничных слоях. слоев. Однородная по и сетка автоматически улавливает рост пограничного слоя вниз по потоку. Дополнительное преимущество состоит в том, что в (15.57) отсутствует нормальная составляющая скорости, т. е. необходимо решать лишь одно уравнение. Значение v при необходимости может быть определено позже. Поскольку на стенке величина Т прямо пропорциональна сдвиговому напряжению (на стенке), метод Дородницына позволяет с большой точностью определить сдвиговое напряжение (11.66).
|
|
© 2003 - 2024 Prom Izhora
При копировании текстов приветствуется обратная ссылка |