

 |
 |
Разделы сайта
Читаемое
Обновления Apr-2024
|
Промышленность Ижоры --> Станки механосборочного производства Сочетание направляющих различных типов в одной конструкции дает возможность использовать положительные свойства различных ВИДОВ трения. Комбинированные направляющие качения-скольжения с облицовкой граней скольжения полимерными материалами имеют хорошие свойства как направляющих качения, так и направляющих скольжения и не имеют их недостатков, т. е. обладают одновременно удовлетворительными характеристиками трения, высокими жесткостью и демпфированием колебаний, являются безударными в наиболее важном направлении и имеют значительно меньшую стоимость, чем направляющие качения. Элементы качения могут быть на основных, боковых или вспомогательных гранях. Остальные грани выполняют как поверхности скольжения. Роликовые опоры на основных горизонтальных гранях применяются в направляющих тяжелых перемещающихся узлов (столы тяжелых фрезерных станков, подвижные стойки тяжелых расточных станков, суппорты тяжелых токарных станков и т. п.); при этом желательно грани скольжения делать с частичной разгрузкой роликовыми опорами, что способствует повышению точности обработки. Направляющие с боковыми гранями качения используют в станках, где в первую очередь необходимо устранить переориентацию узлов при реверсах (расточные, многооперационные, токарные, бесконсольно- и вертикально-фрезерные станки и др.). Общая сила трения в комбинированных направляющих качения-скольжения Г = ro + /cK/Vx + -4/V2, где Го л; 5 Н; /ск - коэффициент трения скольжения, для чугуна /ск = 0,l-f-0,25; / -коэффициент трения качения, для чугуна /к = 0,0025 см, для стали / = 0,001 см; Ni, - доли общей нагрузки, воспринимаемые соответственно направляющими скольжения и качения, Н; г - радиус тел качения, см. Гидроразгрузка направляющих с полужидкостной смазкой за счет подачи в разгружающие карманы масла под давлением весьма эффективна для наиболее ответственных направляющих. Подбором давления масла в карманах можно резко уменьшить коэффициент трения, обеспечить высокую долговечность направляющих, а отсутствие всплывания, которое имеет место в гидростатических направляющих, обеспечивает высокую контактную жесткость и надежную фиксацию узла после перестановки. Сила трения в направляющих с гидроразгрузкой где / - коэффициент смешанного трения; Рд - сила гидроразгрузки. Сила гидроразгрузки та же, что и для гидростатических направляющих, Ро = ряРср-, обычно Ро == 0,7Pjv. Комбинация гидростатических и гидродинамических опор целесообразна при большом диапазоне изменения скоростей, что в направляющих встречается редко. Такие опоры применяют для быстроходных шпинделей станков с большим диапазоном регулирования частоты вращения. Комбинации гидростатических опор и направляющих качения целесообразны в отдельных случаях для создания замкнутых гидростатических опор. Подпружиненные катки могут обеспечить надежное замыкание гидростатических опор даже при отсутствии внешней постоянной нагрузки. Сочетание гидростатических направляющих с аэростатическими возможно в случаях, когда аэростатические опоры выполняют вспомогательные функции уплотняющих устройств. Для силового замыкания аэростатические направляющие малопригодны из-за низкого давления в пневмосети. ГЛАВА 18 РАСЧЕТ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК СТАНКОВ § 1, ДИНАМИЧЕСКАЯ СИСТЕМА СТАНКА Динамический расчет станка необходим для определения показателей динамического качества, используемых затем для оценки производительности и точности станка, сравнительного анализа различных конструктивных вариантов и оптимизации. Наиболее полно вопросы анализа динамики станков рассмотрены в работе В. А. Кудинова, где предложены следующие основные показатели динамического качества станка: запас устойчивостИл-реакция системы на внешние воздействия, быстродействие, определяющее прбдШ1иштёЖТГбсть тгерехбда Запас устой- чивости характеризует возможности изменения того или иного параметра системы (жесткости, скорости движения, линейного размера и др.) без потери ею устойчивости. В роли сигналов, по которым определяются второй и третий показатели системы, могут выступать относительные смещения или скорости движения инструмента и заготовки (при оценке точности обработки), напряжения в нагруженной детали, контактные напряжения (при оценке надежности и долговечности системы), температура нагрева и др. В. А. Куди-новым дано представление о динамической системе станка как замкнутой многоконтурной системе, включающей упругую систему (станок, приспособление, инструмент, заготовка) и рабочие процессы, протекающие в ее подвижных соединениях (резание, трение, процессы в двигателях). С динамической системой станка познакомимся на простом примере. ПрЦ исследовании вынужденных колебаний плоскошлифовального станка можно сделать допущения о бесконечно большой жест- кости подсистемы заготовки, по сравнению с жесткостью подсистемы шлифовального круга, в направлении, перпендикулярном к обрабатываемой поверхности, и о линейности системы. Входными воздействиями на систему станка являются: силовое воздействие и (t) от неуравновешенности шлифовального круга и изменение (t) глубины резания вследствие эксцентриситета круга. Для учета только низкочастотных форм колебаний станка можно представить его системой с одной степенью свободы (рис. 18.1). Приняв в качестве переменной состояния системы изменение q (t) относительного положения шлифовального круга и обрабатываемой заготовки по нормали к поверхности обработки и используя принцип Даламбера, 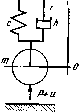 Рис. 18.1. Расчетная схема дина- Рис. 18.2. Структурная схема динамической мической системы станка системы станка получим математическую модель системы в виде обыкновенного дифференциального уравнения mq{i)-{-hq{()-{-cqit) = Pit)-\-u{ty, где т, h, с - соответственно приведенная масса, эквивалентные коэффициенты демпфирования и жесткости подсистемы шлифовального круга (параметры упругой системы станка); Р (t) - изменение силы резания; kj, - коэффициент пропорциональности (характеристика процесса резания). Для систем с большим числом степеней свободы дифференциальные уравнения обычно записывают в матричной форме. Если при нулевых начальных условиях к дифференциальному уравнению (18.1) применить преобразование Лапласа, предварительно поделив все его члены на с, то получим (-f А S -f 1) <у (S) = [Р (S) -f и (S)] -1; P{s) = kp[yt{s)-q{s)], (18.2) где q (s), Р (s), и (s), yt (s) - преобразования Лапласа переменных q (i), Р (t), и (t), yt (t); s - комплексная переменная. Введя обозначения т/с = Л, Ыс = 2gT (t - коэффициент демпфирования) и = \/с, запишем систему (18.2) в иной форме: = T4+2iTs+i + = У 1 + (18.3) Pis)kp[yt(s)q{s)\, где Wa. у. с (s) - передаточная функция эквивалентной упругой системы, включающей, помимо упругой системы, трение. Запись уравнений в форме (18.3) дает возможность представить структуру рассматриваемой динамической системы станка в виде совокупности упругой системы и процесса резания, взаимодействующих между собой (рис. 18.2). Внутри прямоугольников, изображающих основные звенья системы, записаны их передаточные функции (в частном случае - коэффициенты). Стрелки показывают направления воздействий звеньев друг на друга, а также внешние воздействия на систему. Разрешив систему уравнений (18.3) относительно изображения переменной состояния q (s), получим математическую модель станка, позволяющую анализировать влияние внешних воздействий на выход динамической системы станка: kpWa.y.c(s) + i + kpWaZi) = + - где Wy (s) - передаточная функция системы по изменению настройки; Wti (s) - передаточная функция системы по внешнему силовому воздействию. Для линейных систем йтраведлив принцип суперпозиции, по--этому влияние внешних воздействий на выход системы можно рассматривать по очереди. Одним из наиболее распространенных видов динамических моделей являются частотные характеристики. Для большинства входных воздействий частотная характеристика системы может быть получена из соответствующей передаточной функции при замене параметра s на /(о. Например, для передаточной функции Wg.y.c (s), определенной выражением (18.3), частотная характеристика имеет вид 9. у. с Ot) = (1 72(й2)-. /2Г<Й или после разделения на действительную и мнимую части получим W э. у. с - (1 y2 2)2 412720)2 (1 - Г <й2)2 . 42Г2(й2 Графиком частотной характеристики Wg, у. с (/< ) является амплитудно-фазовая частотная характеристика (АФЧХ), которая строится на комплексной плоскости (рис. 18.3, а). Она представляет собой геометрическое место концов векторов (годограф), соответствующих Wa.y.c (/со) при изменении частоты от нуля до бесконечности (или до (Umax)- При а = О Wg.y.c (/ ) = k, Т. 6. податливости упругой системы станка, при со = 1/Т радиус-вектор АФЧХ совпадает с отрицательным направлением мнимой оси, а его величина k/2l зависит от относительного коэффициента демпфирования (для упругих систем станков I = 0,05-И), 15). ;(s) Упругие системы станков, как правило, имеют более сложные АФЧХ, чем системы с одной степенью свободы. На рис. 18.3, б показана экспериментальная АФЧХ одностоечного плЬскошлифо-вальиого станка с горизонтальным шпинделем. Характеристика в диапазоне от О до 700 c имеет три основные резонансные петли (под петлей понимается участок АФЧХ вблизи резонансной частоты). В данном случае первая петля соответствует преобладающим вертикальным колебаниям шлифовальной бабки (частота 125 с~), вторая и третья - двум формам изгибных колебаний шпинделя со шлифовальным кругом. На рис. 18.3, в показана экспериментальная
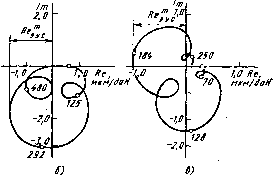 Рис, 18.3. Амплитудно-фазовые частотные характеристики: о - одномассовой упругой системы (см. рнс. 18.1); б - плоскошлифовального станка; в токарного станка АФЧХ токарного стайка средних размеров. Наиболее характерными резонансными петлями характеристики в данном случае являются петли, соответствующие преобладающим колебаниям нижнего суппорта (частота 70 с *), переднего (частота 128 с~*) и заднего (частота 184 с~) концов обрабатываемой детали, верхнего суппорта (частота 250 с-1). АФЧХ упругих систем станков зависит от большого числа факторов: конструкции станка и значения его параметров, режима работы станка, способа закрепления и размеров обрабатываемой заготовки, координат точки рабочего пространства станка и др. Динамические свойства станка можно оценить по величине отрицательного максимума действительной составляющей частотной характеристики разомкнутой системы эквивалентная упругая система - процесс резания ираз (f) = рэ. у. с (Л- На АФЧХ упругой системы станка этой величине соответствует отрезок Re?, у о (рис. 18.3, б). Виброустойчивость станка тем выше, чем меньше отрезок Ref. у. с-Известно, например, что значение предельной стружки /цр (где пр - максимальная глубина резания, при которой обработка на станке идет без вибраций) уменьшается с увеличением Re у. о и наоборот; между ними существует сильная корреляционная связь. Отрезок Re у. с связан с петлей характеристики U?. у. с (/), соответствующей так называемой потенциально неустойчивой форме колебаний упругой системы станка. При обработке с глубиной резания / /пр в станке возникают интенсивные колебания (потеря устойчивости) на частоте потенциально неустойчивой формы колебаний. Эта форма связана в основном с колебаниями определенного узла или элемента стайка, которые являются слабым звеном в его динамической системе. При решении конкретных задач динамики многоконтуриую динамическую систему станка обычно заменяют эквивалентной ей одноконтурной системой. Можно назвать три основных типа таких задач: 1) расчет станка при резании; 2) расчет станка при холостом ходе (например, расчет позиционирования узлов); 3) расчет привода станка. При решении задач первого типа в контур связи включают всего два звена - процесс резаиия и эквивалентную упругую систему (ЭУС). Структурная схема такой одноконтурной системы показана иа рис. 18.2. Направленность связей в системе позволяет при расчете выделять ее звенья и рассматривать их отдельно. В основе решения задач первого типа лежит расчет динамических, характеристик эквивалентной упругой системы станка, процесса резаиия и одноконтурной разомкнутой системы; последняя характеристика служит основой при оценке всех показателей динамического качества станка. В процессе расчета определяют частотные характеристики звеньев и систем, обычно в форме амплитудно-фазовой частотной характеристики. Расчет проводят иа стадии технического проекта, когда конструкция станка проработана достаточно детально и имеется подробная информация о его параметрах и возможных диапазонах их изменения. Расчет можно проводить ие только для оценки показателей динамического качества станка, ион при поиске оптимальной конструкции упругой системы по этим показателям. В этом случае необходима математическая модель системы, адекватная базовому варианту станка. § 2. РАЗРАБОТКА РАСЧЕТНОЙ СХЕМЫ УПРУГОЙ СИСТЕМЫ СТАНКА С точки зрения динамики реальная упругая система станка - это сложная колебательная система с распределенными инерционными и упругими параметрами, имеющая бесконечное число степеней свободы и, соответственно, бесконечное множество собственных частот колебаний. Точный расчет такой системы практически невозможен. При расчете динамических характеристик реальную упругую систему стайка заменяют расчетной схемой, т. е. системой с конечным числом степеней свободы в виде некоторого количества сосредоточенных масс, соединенных невесомыми упругими и диссипа-тивиыми (рассеивающими энергию колебаний) элементами, обычно с линейньми характеристиками. Такое представление системы станка основано иа том, что большинство корпусных деталей - тяжелые и
|
|
© 2003 - 2024 Prom Izhora
При копировании текстов приветствуется обратная ссылка |