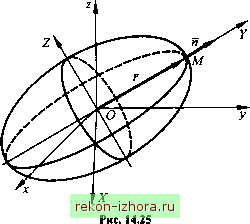с учетом (14.23) уравнения (14.24) преобразуются к виду (- Х)х - Jyy - Jz = 0; -Jy,x + {Jy-X)y-Jy,zQ, (14.25)

->Ух->Л;; + (Л->?1)г = 0.

Система уравнений (14.25) определяет координаты точки M{x,y,z) главной оси инерции (см. рис. 14.25). Ненулевое решение эта система имеет при условии, что

= 0.

(14.26)

Уравнение (14.26) имеет три действительных корня Я , в случае симметричности тензора инерции и действительности

его компонент. Допустим, что все корни различные. Подставив их значения в (14.25), получим три системы уравнений, из которых найдем три точки пересечения главных осей инерции для точки О с эллипсоидом инерции. Из системы уравнений (14.25) при известных А.Д/ = 1,2,3) определим отношения x/z и >/z.H3 первых двух уравнений (14.25) получим решение в форме

X у Z

Л,(Х,) Дз(Х,) А,{Х,У

(14.27)

где АДА ),(7 = 1,2,3) -алгебраические дополнения элементов

последней строки определителя (14.26).

Выражения (14.27) представляют собой уравнения прямых, проходящих через точки 0(0,0,0) и M{x,y,z), и являются

уравнениями главных осей инерции.

Если в системе (14.25) одно уравнение независимое, то любое из уравнений этой системы является уравнением плоскости, в которой лежат главные оси инерции для точки О.

Докажем, что двум различным корням и А. соответствуют два ортогональных направления главных осей инерции. Для А и А координаты точек Л/, и будут соответственно л: Уп и х, у, z.

Из уравнений (14.24) имеем

dF дх

x. +

ду ду

У к +

У, +

г к =>/(Л +У,Ук +2,z)\ Z, =)ii,{x,x +y,y+z,z).

Вычитая из первого уравнения второе, получаем

(X, -Х,){х,х, +у,у, +2,z,)-0. (14.28)

Если X, , то должен быть равен нулю второй множитель в уравнении (14.28). Этот множитель представляет собой скалярное произведение радиус-векторов главных направлений и

Следовательно, их направления ортогональны.

Выберем теперь в качестве осей координат главные оси инерции в точке О, Для оси ОХ имеем У = Z = О и из первого уравнения (14.25) получаем {j - А., ) = О. Здесь X 0, поэтому А =Jx- Аналогично можно показать, что Х2 = Jy, Х = Jy .

Таким образом, корни А. Х2, Х уравнения (14.26) равны соответственно главным моментам инерции , Jy > Jz Для точки О.

Пример 14,6, Для однородной квадратной пластины OABD, масса которой М, а сторона а, определить тензор инерции для осей системы координат Oxyz (рис. 14.26).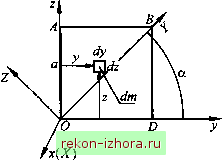

Рис. 14.26

Решение, Моменты инерции относительно осей декартовой системы координат равны

Ма , М ( 2 2\

в точке о Ох- главная ось инерции, так как она перпендикулярна плоскости симметрии пластины, поэтому = = 0.

Определим центробежный момент инерции J = jyzdm . Пусть dm =

= pidydz, где p, = м/\ dm = dydz . Тогда

-y- ]ydydz = -\zdz\ydy = -\ Jy,=J. Тензор инерции имеет вид

Пример 14,7, Для условий предыдущего примера определить главные оси инерции пластины для точки О и главные моменты инерции относительно этих осей.

Решение, Для нахождения главных моментов инерции составим определитель