условии, что центр тяжести тела (точка С) лежит на оси его динамической симметрии OZ, Наглядным примером может служить движение быстровращающегося симметричного тяжелого волчка (А = В\ опирающегося острым носиком на неподвижную точку О (рис. 16.10). Название тяжелый ролчок подчеркивает необходимость учета момента его силы тяжести Р =mg относительно точки О (ОС = /).

Используем (16.11) для вывода дифференциальных уравнений движения волчка. Считаем, что для волчка главный момент внешних сил относительно точки О равен

моменту постоянной силы тяжести Р : Lq =Mq(P) = OCxP. Направим ось Oz вертикально вверх, а ось OZ так, чтобы в системе S = +/. Моменты силы Р относительно осей OZ и Oz постоянно равны нулю: (Р) = (Р) = О.

Получим выражения для моментов силы Р относительно осей ОХ, OY: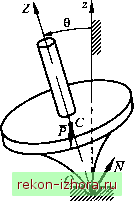

Рис. 16.10

Mq(P) = OCxP =

= -lPyI+lPJ,

Проекции силы Р на оси системы S равны

Р =-Psin0sin9; Ру =-Psin0cos9; Ру =-Pcos0. (16.34)

Поэтому моменты силы Р относительно осей ОХ, ОУ зависят от 0 и ф:

М; =P/sin0cos9; Mj. =-P/sin0sin9, а динамические уравнения Эйлера имеют вид

Ах +(С -А)(0у(02 =P/sin0cos9;

А(Ьу +(A-C)(0z(0x =-P/sin0sin9; (16.35)

т. е. в данном случае уравнения (4.8) и (16.35) необходимо решать совместно. Прямые методы интегрирования этой системы, состоящей из шести дифференциальных уравнений, при произвольных начальных условиях приводят к эллиптическим интегралам. Интегрирование данной системы является принципиально выполненным, если для нее найдены в явном виде четыре независимых первых интеграла. Тогда дальнейшие расчеты сводятся к решению алгебраической системы относительно четырех независимых неизвестных, в роли которых могут выступать проекции угловой скорости тела и какая-либо комбинация тригонометрических функций от углов Эйлера.

К числу трех независимых первых интегралов системы (16.35) относят:

1) интеграл сохранения полной механической энергии

Е = Т+ n = const = EQ,

где П = Pz = PI COS0 - потенциальная энергия тела;

2) интеграл сохранения главного момента количеств движения тела относительно вертикальной оси Oz

=Кок=Кхкх +Куку +Кк = const = К1\

3) интеграл сохранения проекции вектора ш на ось динамической симметрии

со = const = а)(. (16.36)

Второй из указанных интегралов следует из теоремы об изменении вектора Kq, записанной в проекции на неподвижную

ось Oz, поскольку М(Р) = 0, а третий - из последнего уравнения системы (16.35).

Для кинематических уравнений Эйлера первым интегралом

служит соотношение к = к\ + к + к = \, удовлетворяющее

дифференциальному уравнению - = -Шхк, полученному для

неподвижного орта к на основании формулы Бура для двух систем Sq и iS, и отражающее постоянство модуля орта к .

Наличие четырех интегралов указывает на существование при произвольных начальных условиях общего аналитического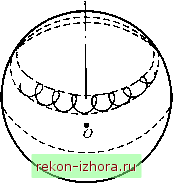

решения для углов Эйлера. Однако это решение может быть записано лишь через эллиптические функции.

Представление о характере движения центральной оси динамической симметрии волчка при достаточно большой угловой скорости собственного вращения можно получить с помощью рис. 16.11, где показан след одной из ее точек, оставляемый на неподвижной сфере. Поскольку направление этой оси определяется углами прецессии v/ и нутации 0, данный след отражает только их изменение. След не имеет точек возврата и петель самопересечения, пока сохраняется знак vj/. Рис. 16.11 Отметим, что к данному случаю

также относится пространственное движение маятника, подвешенного на одной неподвижной точке. Его движение может быть неравномерным вращением - ротацией вокруг неподвижной горизонтальной оси - или периодическими колебаниями - осцилляцией в окрестности нижнего положения равновесия. Последний вариант движения имеет маятник, отпущенный из состояния покоя, при котором ось динамической симметрии отклонена от вертикали. Еще один несложный вариант движения тела в случае Лагранжа - равномерное вращение вокруг вертикальной оси динамической симметрии, когда центр масс расположен ниже точки подвеса. Если центр масс расположен выше точки опоры, то вертикальное направление оси динамической симметрии устойчиво лишь при достаточно быстром вращении ( спящий волчок ).

Предыдущая схема анализа движения тела в случае Лагранжа относилась к произвольным начальным условиям. Существует простое решение данной задачи, но для специальных начальных условий. При этом движение волчка внешне выглядит как регулярная прецессия, в связи с чем оно названо псевдорегулярной прецессией.