то рассматриваемое положение равновесия называется асимптотически устойчивым.

Достаточное условие устойчивости положения равновесия консервативной системы определяется теоремой Лагранжа: достаточным условием устойчивости положения равновесия консервативной системы является наличие в нем локального {изолированного) минимума потенциальной энергии.

Однако в реальной механической системе всегда существуют силы сопротивления движению, возникающие благодаря трению или вязкости среды. Такие силы Кельвином названы диссипа-тивными.

При наличии в системе диссипативных сил для оценки устойчивости положения равновесия можно дополнительно воспользоваться тремя теоремами Кельвина.

1. Если положение равновесия консервативной системы устойчиво при одних только потенциальных силах, то оно будет оставаться устойчивым и при добавлении диссипативных сил.

2. Устойчивое положение равновесия становится асимптотически устойчивым при добавлении диссипативных сил с полной диссипацией .

3. Изолированное и неустойчивое при одних потенциальных силах положение равновесия не может быть стабилизировано диссипативными силами.

Доказательства этих теорем могут быть получены как следствие теоремы Ляпунова об устойчивости движения, выходящей за рамки данного курса.

Первые две теоремы Кельвина указывают на то, что дисси-пативные силы не могут нарушить устойчивость положения равновесия, а третья - что диссипативные силы не в состоянии трансформировать неустойчивое положение равновесия консервативной системы в устойчивое. Следовательно, для оценки устойчивости положения равновесия реальную колебательную систему с диссипативными силами можно заменить ее консервативной моделью.

Понятие полной диссипации существенно для систем с числом степеней свободы п > 1 и будет определено в § 19.7.

19.2. Дифференциальные уравнения малых колебаний линейной системы с одной степенью свободы

Отметим, что наличие в механической системе хотя бы одного упругого (деформируемого) тела автоматически превращает ее в систему с бесконечным числом степеней свободы, поскольку у таких тел каждая материальная частица имеет возможность двигаться относительно других материальных частиц и, следовательно, ее движение должно описываться своими обобщенными координатами, а таких частиц бесконечное множество.

В теоретической механике используется модель абсолютно твердого тела, для описания движения которого требуется конечное число координат, а все упругие элементы - пружины принимаются безынерционными, т. е. масса их считается пренебрежимо малой по сравнению с массами твердых тел, входящих в систему. Только в этом случае можно говорить о системе с конечным числом степеней свободы. Рассмотрим несколько примеров.

Пример 19.1. Тело массой /и, подвешенное к пружине АВ (рис. 19.2, f), движется поступательно в вертикальном направлении под действием силы

F(t), преодолевая вязкое сопротивление среды. Составить уравнение малых колебаний.

Решение. На рис. 19.2, б представлена зависимость реакции F цилиндрической пружины растяжения - сжатия от деформации X. Предположив, что деформации пружины относительно малы, т. е. мала амплитуда колебаний тела, характеристику пружины можно аппроксимировать наклонной прямой, тангенс угла а наклона которой называется коэффициентом жесткости, или просто жесткостью с пружины.

При сделанном допущении о малых деформациях пружины линейная восстанавливающая сила будет противоположна по направлению деформации пружины:

Г = сА.. (19.2)

На рис. 19.2, в представлена зависимость силы вязкого сопротивления среды F от скорости движения в ней тела v . Только при достаточно малых скоростях движения тела можно аппроксимировать характеристику наклонной прямой, тангенс угла наклона у которой называется коэффициентом линейного вязкого сопротивления h и имеет единицу измерения ньютон-секунда на меар (Нс/м). При сделанном допущении о малых скоростях движения тела сила вязкого сопротивления

Fhv,

всегда линейна и направлена противоположно скорости движения тела.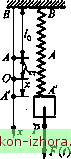

Рис. 19.2

Если AB=Iq (см. рис. 19.2, а) длина нерастянутой пружины, то АО представляет собой статическое удлинение пружины под действием силы тяжести

тела, равное

(19.3)

Будем отсчитывать координату х от положения статического равновесия О, тогда дифференциальное уравнение поступательного движения тела имеет вид

тх = F{t) + - с(Хст + л) - /юс. (19.4)

В силу (19.3) mg и ск взаимно уничтожаются, и уравнение (19.4) принимает вид

m5f + Ax+cx = F(0. Если Fit) = Fo sin(pr+Р), то

mic+Ах+сх = Fq sin(pr+Р) ,

x+2ех+шх = /о sin(p/ + р), (19.5)

где 28 = him, = с/т, /о Р/т,