Пример 19.2. Однородный диск А, момент инерции которого J, через упругий безынерционный стержень скреплен с телом В, вращающимся по закону

v/(0 = Мо sm{pt + р) (рис. 19.3). Составить уравнение малых колебаний диска.

Решение. Выберем в качестве координаты угол поворота ф и составим дифференциальное уравнение вращательного движения диска (ось Oz при этом остается прямолинейной). Полагая, что ф > vj/, а сами углы ф и v;/ малы, запишем выражение для момента М (см. рис. 19.3) в виде Af = с[ф-У/о sin(/7r + p)],

где с - жесткость стержня на кручение.

При вращении однородного диска вязкое сопротивление среды мало и его можно не учитывать. Тогда дифференциальное уравнение вращательного движения диска будет иметь вид Jcp = = -с[ф - Vj/o sm{pt + Р)],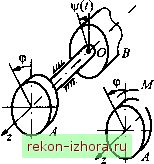

Рис. 19.3

Ф + юФ = /о8т(/7Г + р),

(19.6)

где (0 =c/J;fQ=c\\fQ/J.

Пример 19.3. Материальная точка (бусинка) массой т закреплена на струне, имеющей предварительное значительное натяжение Т (рис. 19.4). Учитывая

вязкое сопротивление среды, составить уравнение малых колебаний. Изменением натяжения струны при движении бусинки, массой струны и влиянием силы тяжести бусинки пренебречь.

Решение. Полагая, что колебания бусинки малы (х /), можно записать sina х/1.

Принимая вязкое сопротивление среды линейным: f* = hx , получим дифференциальное уравнение движения бусинки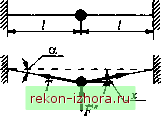

Рис. 19.4

/пх =-2Г sina - =-2Г--/IX,

х + 2&х + юх = 0.

(19.7)

где 28 = /г/,ю=2Г/т/.

Приведенные примеры показывают, что при сделанном допущении о малости колебаний, колебательные системы описываются одинаковыми по структуре линейными дифференциаль-

ными уравнениями (19.5) - (19.7). Они могут быть полными (см. 19.5), в них может отсутствовать обобщенная скорость (при пренебрежении силами вязкого сопротивления (см. 19.6)) или правая часть (в случае отсутствия вынуждающей силы (см. 19.7)). Однако условие малости колебаний еще не гарантирует линейность дифференциальных уравнений. Так, при учете сил сухого трения дифференциальное уравнение остается нелинейным даже при сделанном допущении.о малости колебаний.

Получим теперь дифференциальное уравнение малых колебаний в общем случае. Рассмотрим механическую систему, состоящую из N материальных точек и имеющую одну степень свободы, на которую наложены голономные, стационарные и неосвобождающие связи. Предположим, что система имеет устойчивое положение равновесия, от которого будем отсчитывать обобщенную координату q,

В соответствии с предположением о малости колебаний обобщенную координату, ее скорость и ускорение полагаем величинами первого порядка малости. В дифференциальных уравнениях движения будем учитывать величины первого порядка малости, а в выражениях для кинетической энергии Г, потенциальной энергии П и вводимой ниже диссипативной функции Рэлея Ф - величины до второго порядка малости, поскольку использование уравнения Лагранжа второго рода

приводит вследствие дифференцирования к понижению порядка малости на единицу.

В общем случае сила, действующая на к-\о точку системы, может быть функцией от положения точки , ее скорости и времени t:

С учетом малости колебаний представим в виде

F,=F;(F,) + F;(v,)-bP,(0, (19.8)

где все силы F/(F) - потенциальные, и будем полагать, что силы F/(v) являются диссипативными, т. е. уменьшающими

полную механическую энергию, и линейно зависящими от скорости:

F;;=-h,v,. (19.9)

Кинетическая энергия системы

В силу стационарности наложенных на систему связей радиус-векторы точек зависят только от обобщенной координаты: h Тогда

и, следовательно, кинетическая энергия

q=\A{q)e

(19.10)

(19.11)

Здесь A{q), как и , является в общем случае функцией обобщенной координаты q.

Разложим A(q) в окрестности положения равновесия (9 = 0) в степенной ряд:

A(q) = A(0) +

(19.12)

Индексом О здесь и далее отмечены величины, вычисленные в положении равновесия.

В силу малости колебаний в выражении (19.11) для кинетической энергии будем учитывать величины не выше второго порядка малости. Но в этом уравнении уже содержится квадрат

обобщенной скорости q - величина второго порядка малости,

поэтому в разложении (19.12) удерживаем только первый член, который обозначаем

А(0) = а.

Коэффициент а называется обобщенным инерционным коэффициентом. Его единица измерения определяется единицей измерения обобщенной координаты: если 9 в м, то а в кг, если в рад, то а в кг м.