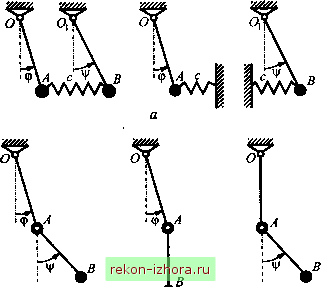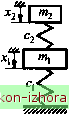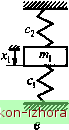Рис. 1930

Подставив (19.98) в (19.95) и сократив на sin(a)/ + a), получим однородную относительно Aj и алгебраическую систему

(Си -СОЧ1М1 +(2 -(ОЧ2М2 (Ci2 -0)a,2)Ai +(С22 ~ 0)22 )А2 =0.

Поскольку однородная алгебраическая система всегда имеет нулевое решение (А =0, А2 =0), а любая невырожденная алгеб-

(19.99)

раическая система имеет единственное решение, то для того чтобы система (19.99) имела ненулевое решение, она должна быть вырожденной, т. е. ее определитель должен равняться нулю:

(Сп -C04l) (12 -0)42)

(С12-СОЧ2) (<22-0)42)

= 0. (19.100)

Следовательно, решение (19.98) будет иметь смьюл не при любых значениях со, а только при тех, которые удовлетворяют условию (19.100).

Раскрывая (19.100), получим

(сц -co4i)(c22 -соЧ2)-(12 -С0Ч2) =0 (19.101)

(1122 -п)® -(qi 22 +2211 -2Ci2 12)c0 +122 4 =0-

(19.102)

Уравнение, представленное в форме (19.100) - (19.102), называют частотным. Как следует из (19.102), частотное уравнение биквадратное. Обозначим его корни в порядке возрастания

через cof и cOj. Важно убедиться, что оба корня положительные, ибо в противном сл)ае (если один или оба корня окажутся отрицательными) частоты cOj и СО2 (или одна из них) будут мнимыми. Такой аргумент в решении (19.98) приведет к трансформации тригонометрического синуса в гиперболический и, следовательно, к неограниченному возрастанию во времени и 2 что противоречит предположению об устойчивости положения равновесия.

Введем функцию А(со), равную левой части частотного уравнения (19.101) или (19.102), т. е.

A(co) = (cii -co4i)(22 -0)42)-(12 -coЧ2)

A(co) = (aiia22-alW-icxciii С22аи-2су2а2) +1122 4 и построим ее график.

Если положение равновесия устойчивое, то в силу (19.97)

А(0) = 1122 - с2 > о. Если = = cJa, то

A(n) = -

если CO =nl =C22/22 TO

2-12

<0,

<0.

22 У

Наконец, в силу того, что ii22~n>0, при юоо

График функции А(о)) в предположении, что щ<П2, представлен на рис. 19.31.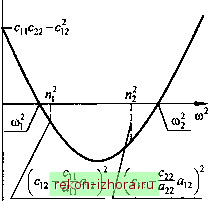

Рис. 1931

Найденные из (19.100)-(19.102) значения ю называют габ-ственными частотами колебаний системы. Собственные частоты системы нумеруют в порядке возрастания, они не зависят от начальных условий и полностью определяются параметрами колебательной системы (квазиупругими и обобщенными инерционными коэффициентами).

Из рассмотренного следует:

1) если положение равновесия устойчивое, то оба корня частотного уравнения положительные;