mx = F +X{df/dx);

my = Fy+X(df/dy); (13.8)

mz = F,+X(df/dz),

известные как уравнения Лагранжа первого рода.

В случае движения по негладкой поверхности необходимо учитывать действие связи на материальную точку в плоскости, перпендикулярной нормали. Если оно обусловлено шероховатостью поверхности связи, то в векторном уравнении движения добавляется сила сухого трения, предельное значение которой при vO определяется выражением

F =-iiXgrad(f)-, V

где ц - коэффициент трения скольжения.

Три дифференциальных уравнения (13.8) и уравнение связи (13.6) содержат четыре неизвестные функции, следовательно, решение возможно. Однако в декартовых координатах при произвольном выборе системы отсчета аналитическое решение задачи удается получить лишь для простейших связей первого порядка. Более эффективными в ряде случаев являются уравнения движения точки в криволинейных координатах. Особенно удобно при этом пользоваться такой системой координат, в которой поверхность связи, определяемая уравнением (13.6), выступает в качестве одной из координатных поверхностей.

Пусть, например, точка движется по внутренней гладкой поверхности цилиндрической трубы (рис. 13.3), уравнение которой в декартовых координатах будет

В цилиндрических координатах уравнение примет вид

/(Г,ф,2) = Г -Г = 0,

а сама поверхность трубы будет координатной поверхностью. Вектор-градиент ее направлен по радиусу, и, следовательно, проекции нормальной реакции на две другие координатные оси равны нулю. Сила тяжести Р - nig. Уравнения движения точки принимают вид

mri = -mgs\ni\ mz = 0; тгф =-mgcos(f> + N. (13.9)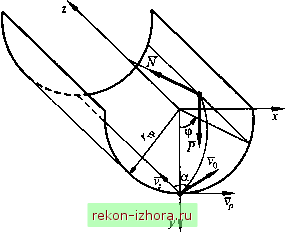

Рис. 13.3

С решением этой системы уравнений связана смешанная задача динамики точки: сначала на основе первого и второго уравнений по активным силам и начальным условиям определяется движение точки (вторая задача динамики точки), а затем из третьего уравнения определяется динамическая реакция N (первая задача динамики точки).

Пример 13.4. Материальная точка массой т начинает движение по гладкой внутренней поверхности трубы радиусом из крайнего нижнего положения с

начальной скоростью Vq , вектор которой расположен в касательной плоскости под углом а к образующей поверхности трубы (см. рис. 13.3). Определить, при каких условиях точка будет двигаться, не покидая стенок трубы.

Решение. Неудерживающая связь, налагаемая на точку стенкой трубы, выражается в цилиндрических координатах неравенством г-г>0 и находится в

напряжении (действует), если N>0 . Как видно из третьего уравнения системы (13.9), является функцией координаты ф и ее производной. Выполнив в первом уравнении (13.9) замену независимой переменной ф = ф(cftp/dicp), разделим переменные и найдем первый интеграл

ф72 = С + (/г)со8ф. В соответствии с начальными условиями движения (при ф = О ф = Фо = = Vq sina/rp ) произвольная постоянная интегрирования

С = Ф?/2-я/г.

Подстановка полученного выражения в третье уравнение (13.9) дает зависимость

Л = тгрф -mg(2-3cos9).

Точка при движении будет оставаться на внутренней поверхности тр>бы. если в любом ее положении, в том числе и в крайнем верхнем, при ф = я ( со5ф = -1 ). Л > О . Отсюда получаем

трФо = (0 sina)- /г,р > 5g . или уДО) > [Sgr ,

где уДО) = Уо51па - начальное значение трансверсальной проекции скорости точки.

Расчеты показывают, что. если условие p{0)>j5gn выполнено, точка

никогда не отделится от стенок трубы и движение ее будет длиться вечно. Такой рез\льтат. несогласующийся с опытом, объясняется несовершенством принятой расчетной схемы, а именно идеализацией свойств связи. Если же принять во внимание шероховатость поверхности трубы, то в первом и втором уравнениях (13 9) нужно учесть проекции силы сухого трения

Тогда эти уравнения примут вид

тгрЦ> =-mgsm(p-[iN .- -; mz--\xN-

pV(r,(pf (i)4(r,p9)-

а ;V будет определяться третьим уравнением системы (13.9).

Нелинейные уравнения этой системы являются связанными, так как все три функции - две координаты (г, ф ) и сила N - присутствуют в каждом из уравнений. Система уравнений может быть проинтегрирована только численно при конкретных значениях параметров, при этом обе задачи динамики точки здесь не разделяются, а решаются параллельно.

Если движение точки стеснено двумя связями вида (13.6), векторное уравнение движения с неопределенными множителями принимает вид

dv -

т- = F + A.,grad (/,) + A.2grad(/2). at

Интегрирование системы скалярных уравнений, включающей три дифференциальных уравнения и два уравнения связи, принципиально возможно, но практически весьма затруднительно. Решение таких задач целесообразно проводить на основе дифференциальных уравнений движения точки, записанных в проекциях на естественные оси.